Algunos consejos para que tu estudio sea más fructífero.
Y si esto no es suficiente, Sigue leyendo «Métodos de estudio»
Categoría: 2ºESO
Articidad (Proyecto sobre Publicidad)
Os dejo el .pdf para que podáis consultar los puntos de los que se compone el proyecto
Comenzando a utilizar Google SketchUp (Parte 1)
Ahora que estamos trabajando las diferentes perspectivas, es el momento de comprobar cómo la tecnología puede sernos de gran utilidad.
Una aplicación que cumple con creces esta necesidad es Google SketchUp. Tienes la posibilidad de trabajar descargando el programa o desde tu propio navegador, para ello, lo primero que debes hacer es clic en «Comenzar a modelar»
A continuación se abrirá una pantalla para que introduzcas tu usuario. Si tienes una cuenta Google ya lo tienes (si tienes un teléfono android también tienes una). Sigue leyendo «Comenzando a utilizar Google SketchUp (Parte 1)»
Planos y angulaciones
Dentro del tema de La representación de la realidad, vamos a ver los diferentes encuadres con los que podemos delimitar la propia Realidad
Una vez visto el video ya tenemos claro los diferentes tipos de plano y para qué se utilizan. Ahora deberías utilizar ese conocimiento para completar esta ficha con las capturas de pantalla de tu película, serie favorita… (o cómic!).
Aquí os dejo un video de Meik donde nos enseña cómo se aplican estos planos al mundo del cómic
Plantilla formato WORD (descárgala pulsando el botón derecho del ratón, y luego en Guardar enlace como)
Plantilla formato docs de Google (Hazte una copia para poder editarla)
Aquí os dejo un ejemplo de Alejandro Quiroga del curso 20/21
¿Eres capaz de indicarme el nombre de los planos y angulaciones de al menos 5 de los 100 mejores planos del cine y explicar brevemente qué sensaciones te transmiten?
Perspectiva Caballera
La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los elementos paralelos a él, están en verdadera magnitud. Como todas las perspectivas nos ayuda a visualizar sobre el plano, los volúmenes que tienen 3 dimensiones.
En perspectiva caballera, dos dimensiones del volumen a representar se proyectan en verdadera magnitud (el alto y el ancho) y la tercera (la profundidad) con un coeficiente de reducción. Las dos dimensiones sin distorsión angular con sus longitudes a escala son la anchura y altura (x, z) mientras que la dimensión que refleja la profundidad (y) se reduce en una proporción determinada. 1:2, 2:3 o 3:4 suelen ser los coeficientes de reducción más habituales.
Los ejes X y Z forman un ángulo de 90º, y el eje Y suele tener 45º (o 135º) respecto a ambos. Se adoptan, por convención, ángulos iguales o múltiplos de 30º y 45º, dejando de lado 90º, 180º, 270º y 360º por razones obvias.
Se puede dibujar fácilmente un volumen a partir de una vista lateral o alzado, trazando a partir de cada vértice líneas paralelas a Y, para reflejar la profundidad del volumen. Puede ser un poco más complicado a la hora de representar elementos curvos, pero es fácilmente solucionable inscribiendo dichos elementos en cuadrados y sacando los puntos intermedios.
Este tipo de proyección es frecuentemente utilizada por su facilidad de ejecución, aunque el resultado final no da una imagen tan real como la que se obtendría con una proyección cónica.
Ahora que está familiarizado con este tipo de perspectiva, responde:
- ¿Cuál de las siguientes imagenes utiliza la perspectiva caballera?
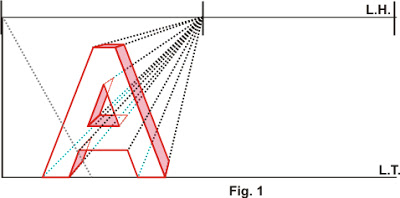
Ahora toca aplicar esta perspectiva estudiada en la siguiente lámina.
Curvas técnicas// Technical curves
Los enlaces son un tema apasionante en el que ahondaremos más adelante, pero por ahora vamos a ver cómo usar las tangencias entre curvas para el trazado de las siguientes curvas técnicas
- Óvalo: // Oval: Es una curva cerrada y plana compuesta por un número par de arcos de circunferencia enlazados entre sí y simétricos respecto sus ejes mayor y menor normales entre sí. (Trazado dado el eje mayor)
Trazado del óvalo dado el eje menor:
- Ovoide // Ovoid: Curva cerrada y plana, compuesta por arcos de circunferencia tangentes entre sí, dos arcos de igual radio y otros de radio distinto, siendo el mayor de ellos, una semicircunferencia. Tiene un solo eje de simetría, que contiene a los centros de los arcos desiguales (Trazado dado el eje menor)
Trazado dado el eje mayor
- Espiral // Spiral: Es una curva plana, abierta, generada por un punto P, situado en el origen O de una semirrecta que se desplaza sobre ella con un movimiento longitudinal, al mismo tiempo que la semirrecta gira alrededor de O con un movimiento circular. Espira // Spira: Cada vuelta de la curva, es decir, el el fragmento de curva generada por un giro de 360º de la semirrecta. Paso// Step: Avance longitudinal de P sobre la semirrecta, entre el origen y fin de cada espira
- Espiral de dos centros
- Espiral de 3 centros
Simetría // Symmetry
La simetría en las formas se refiere a la correspondencia exacta en tamaño, forma y posición de las partes de un todo respecto a un eje. Por lo tanto, una imagen simétrica es aquella donde una parte de la misma, por repetición configura el todo. //
Symmetry in shapes talk about the exact correspondence in size, shape and position of the parts of a whole with respect to an axis. Therefore, a symmetric image is one where a part of it, by repetition configures the whole
Más adelante veremos los distintos tipos de simetría que existen.
¿Alguna vez has escuchado eso de «éste es mi perfil bueno»?
Algunos famosos sólo permiten que se les grabe desde un determinado punto de vista porque aseguran que tienen un perfil bueno y otro menos bueno (Uno de los casos más sonados fue cuendo Isabel Preysler cambió el sitio a Pablo Motos en su entrevista para el Hormiguero) //
Some artist says that they have a «good side» and only allow show this side in their interviews (Like Isabel Preysler did in El Hormiguero)
No está lejos de la realidad, y es que, aunque en apariencia somos simétricos… la cosa dista bastante de uno a otro
La cosa cambia bastante, ¿verdad?
Hilma af Klint
La mayoría de libros de Arte, ya sean libros de texto para Secundaria o Bachillerato, colocan a Vassily Kandinsky como el creador de la «Abstracción Geométrica» ya que él mismo se autoproclamó como su creador en su libro «De lo espiritual en el Arte» (1911)
Pero resulta que ya hubo quien jugaba con la abstracción de las formas antes que él. Sigue leyendo «Hilma af Klint»
Pentágono regular
Ahora veremos el trazado de un pentágono regular inscrito en una circunferencia dada.
A continuación, un pentágono regular dado el lado.
Feliz trazado!!
Parque Jurásico
Como proyecto de fin de curso, en el taller de Manualidades, y con la colaboración del alumnado de Tercero de EPVA, nos hemos currado un Parque jurásico con dinosaurios de origami y un diorama realizado con materiales reciclados.
¡Gracias a tod@s l@s que habéis participado en su creación!
Plasticavite.com 