Cuadrilateros // Quadrilaterals
Categoría: Sin categoría
Recursos fotocopiables
Polígonos regulares inscritos
Por si acaso la perdiste, aquí tienes la lámina para descargarla
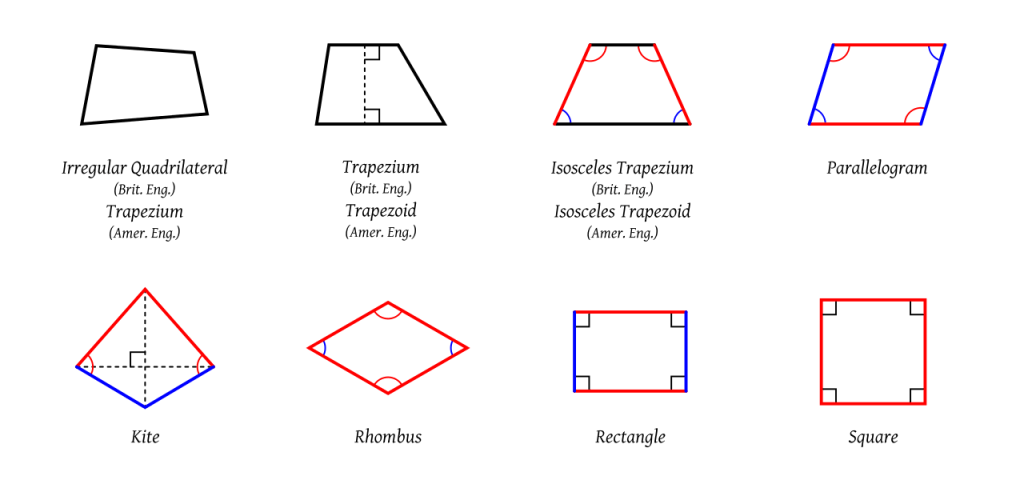
Antes de nada, recordaros que empezamos el ejercicio conociendo el radio de la circunferencia en la que se inscribe el polígono. Seguro que sabéis que el hexágono es el único polígono cuyo lado es igual al radio de la circunferencia en el que se inscribe, por lo que no hace falta ningún trazado auxiliar para su resolución.
Ahora sí, vamos con el resto de polígonos.
Trazado de triángulo equilátero inscrito en una circunferencia
Cuadrado inscrito en una circunferencia
Pentágono
La lámina de los polígonos debería quedar algo así
Si quieres avanzar en polígonos más complejos, cada uno tiene su propio método, pero existe uno que te puede facilitar el trabajo en caso de ir más justo de memoria.
Método general para el trazado de polígonos regulares inscritos
2º ESO Lámina 1
DESPUÉS DE VER CÓMO SE USA LA ESCUADRA Y EL CARTABÓN, PASAREMOS A LA ACCIÓN.
Recuerda que las propuestas son orientativas, trata de no copiar los ejemplos y busca tu propia alternativa a los trabajos.
ACTIVIDAD 2º ESO:
- Traza sobre tu espacio de trabajo una serie de líneas paralelas y perpendiculares (con cualquier inclinación, no es obligatorio que lleguen al margen, pero sí que sean perfectamente perpendiculares entre sí)
- Dibujar el contorno de una figura, letra o número que tú elijas.
- Da color alternando los recuadros adyacentes y cambia de gama de color al llegar al interior del contorno
Galería de trabajos de 2º
SOS // Apoyo // Refuerzo
Si necesitas una ayudita para empezar a trabajar prueba a imprimirte estas láminas!
Margen y Cajetín
Antes de meternos en materia debemos hacer una serie de trazados en nuestra lámina para poder organizar adecuadamente nuestro trabajo.
Lo primero será hacer el margen, que delimitará nuestro espacio de trabajo en la lámina. Éste margen ed de 1 cm arriba, abajo y a la derecha. A la izquierda es de 2 cm, con idea de poder hacer las perforaciones correspondientes para su encuadernado.
A continuación habrá que crear nuestro Cajetín, donde indicaremos los siguientes datos:
- Fecha
- Nombre y Apellidos
- Curso
La altura del cajetín es de 1,5 cm y tiene una anchura de 3, 12 y 3 cm respectivamente.
Todas los trabajos de este curso deberán realizarse en láminas con su correspondiente Margen y Cajetín (salvo que se indique lo contrario).
Lámina 1. Paralelas y perpendiculares
Después de ver cómo se usa la escuadra y el cartabón, pasaremos a la acción.
Recuerda que las propuestas son orientativas, trata de no copiar los ejemplos y busca tu propia alternativa a los trabajos.
Actividad 1º ESO:
- Divide tu espacio de trabajo EN CUATRO PARTES IGUALES.
- En cada uno de esos espacios deberás disponer líneas paralelas separadas 1 cm entre sí, en diferentes direcciones (unas verticales, otras horizontales, unas con 30º de inclinación y otras con 45º)
- Dibujar el contorno de una figura, letra o número que tú elijas en cada uno de los espacios.
- Da color alternando con el blanco (o con cualquier otro color) a las líneas paralelas y cambia el orden cuando llegues a la línea de contorno)
Galería de trabajos de 1º
SOS // Apoyo // Refuerzo
Si necesitas una ayudita para empezar a trabajar prueba a imprimirte estas láminas!
Flatland
¿Te imagina que vives en un mundo en dos dimensiones?
Sabes que hay una tercera dimensión por tu experiencia, pero… y si hubiera más?
En 1884 Edwin Abbott escribió Planilandia, donde describe un mundo en dos dimensiones donde todo se mide en altura y anchura. Abbott es capa de resolver cualquier problema que pueda plantearse para los habitantes de ese mundo, hasta que una esfera entra en juego.
De Flatland se han hecho diferentes cortos y adaptaciones, pero en esta charla TED creo que explican muy claramente el planteamiento.
Aquí os dejo el trailer de Flatland The Movie de 2007 de Dano Johnson & Jeffrey Travis
Casualidades de la vida, en 2007 también salió a la luz otro Corto llamado Flatland (Ladd Ehlinger Jr.) que podemos ver íntegramente en Youtube
Análisis del segundo corto en Pensar el Cine
Red Modular (lámina doble) 2025-26
Para este trabajo tenemos que saber qué es una red modular.
Podemos definir una Red Modular como una estructura donde se repite una imagen de manera indefinida hasta completar una superficie. Se entiende que una red modular puede ser bidimensional o tridimensional, natural o artificial, simple o compuesta, etc. según sus características, como ya vimos en la entrada de Redes modulares de 1º de la ESO.
Una vez conocidas sus características, vamos a estudiar los movimientos que podemos aplicarle al módulo (imagen que se repite), para crear diferentes patrones utilizando la misma imagen base.
- Traslación: el módulo se repite en la misma posición que el original
La circunferencia
Definición y elementos básicos de la circunferencia
¿Qué es una circunferencia?
De manera formal, una circunferencia se define como el lugar geométrico de los puntos del plano equidistantes de otro, llamado centro de la circunferencia.//
A circunferemce is the set of all points in the plane that are the same distance away from a specific point, called the center
No debemos nunca confundir el concepto de círculo con el concepto de circunferencia, que en realidad una circunferencia es la curva que encierra a un círculo (la circunferencia es una curva, el círculo una superficie). Sigue leyendo «La circunferencia»
La percepción visual (II)
Las figuras imposibles// Impossible objects
Desde el Renacimiento este tipo de imágenes han sido utilizadas para sorprender al espectador con mundos imposibles. Por ejemplo, en el siglo XVIII el arquitecto y dibujante italiano Giambattista Piranesi (1720-1778) publicó una serie de litografías titulada “Carceri d’invenzione” en las que dibujaba cárceles inventadas formadas por espacios irreales con enormes y oscuros pasadizos, empinadas escaleras a grandes alturas y extrañas galerías que no llevan a ningún sitio.//
Since the Renaissance this type of images have been used to surprise the viewer with impossible worlds. For example, in the 18th century the Italian architect and draftsman Giambattista Piranesi (1720-1778) published a series of lithographs entitled «Carceri d’invenzione» in which he drew up invented prisons formed by unreal spaces with huge and dark passageways, steep stairs to great heights and strange galleries that don’t lead anywhere.
Plasticavite.com 