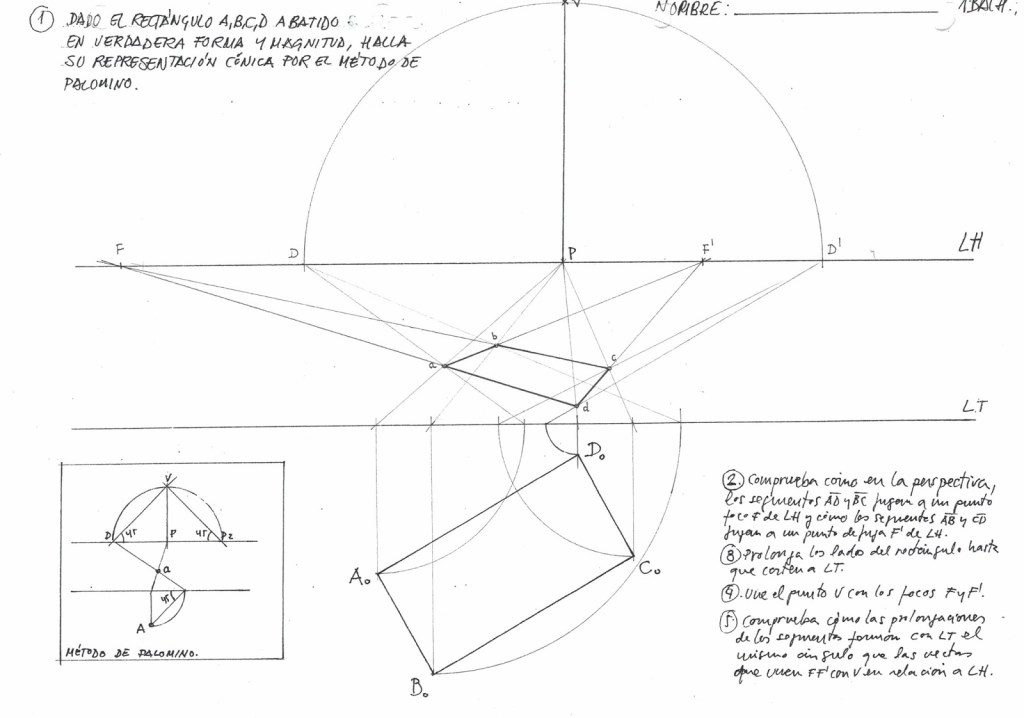
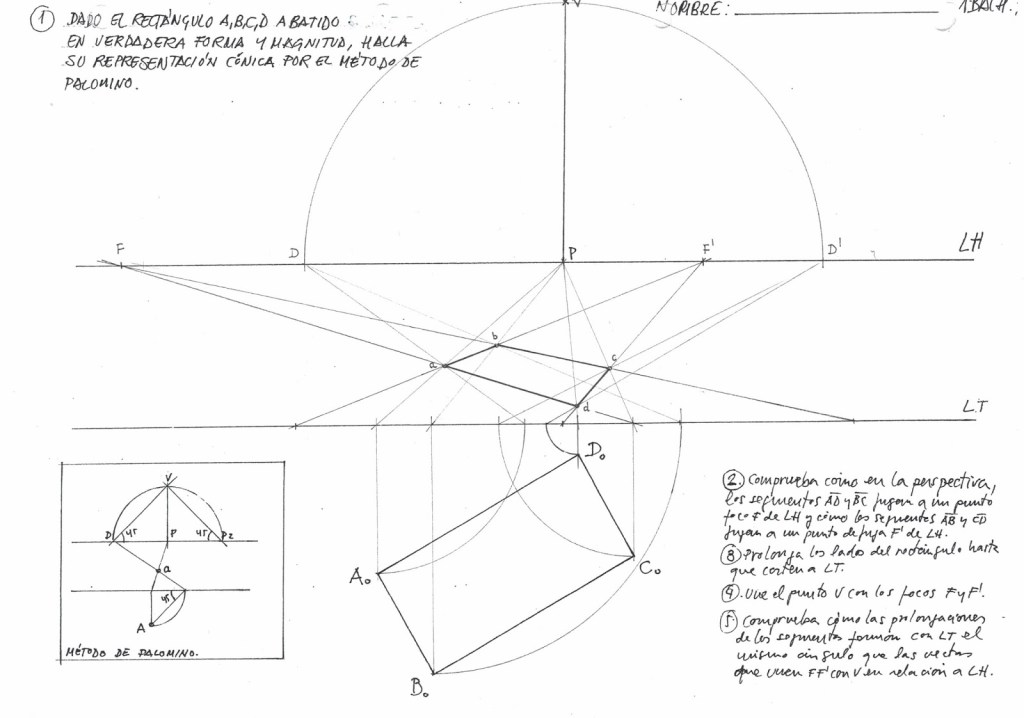
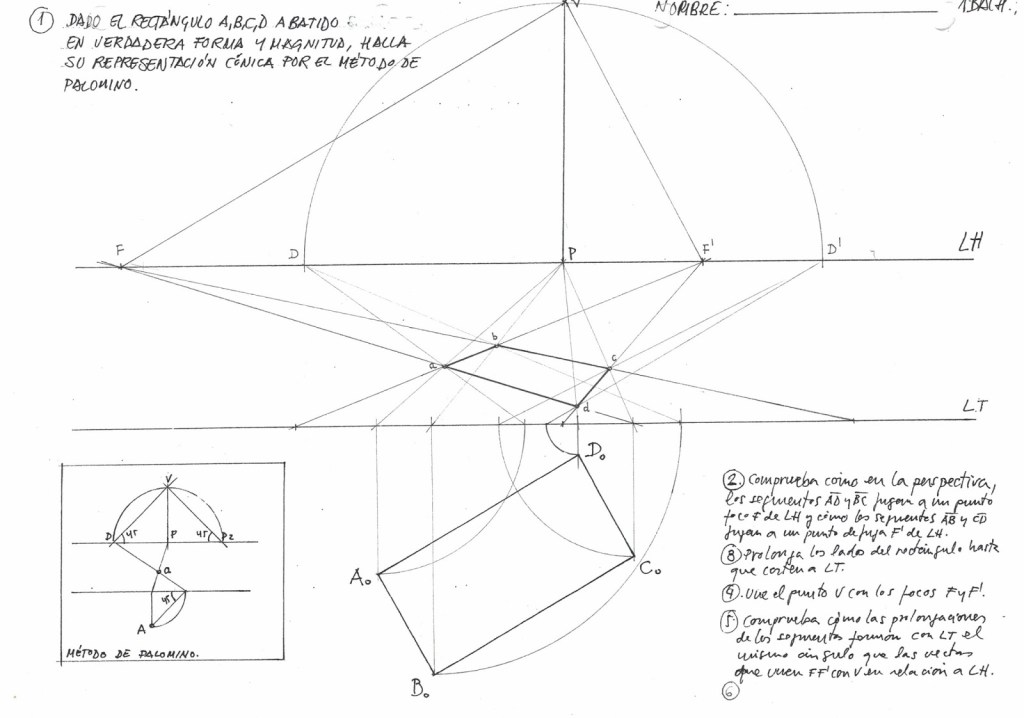
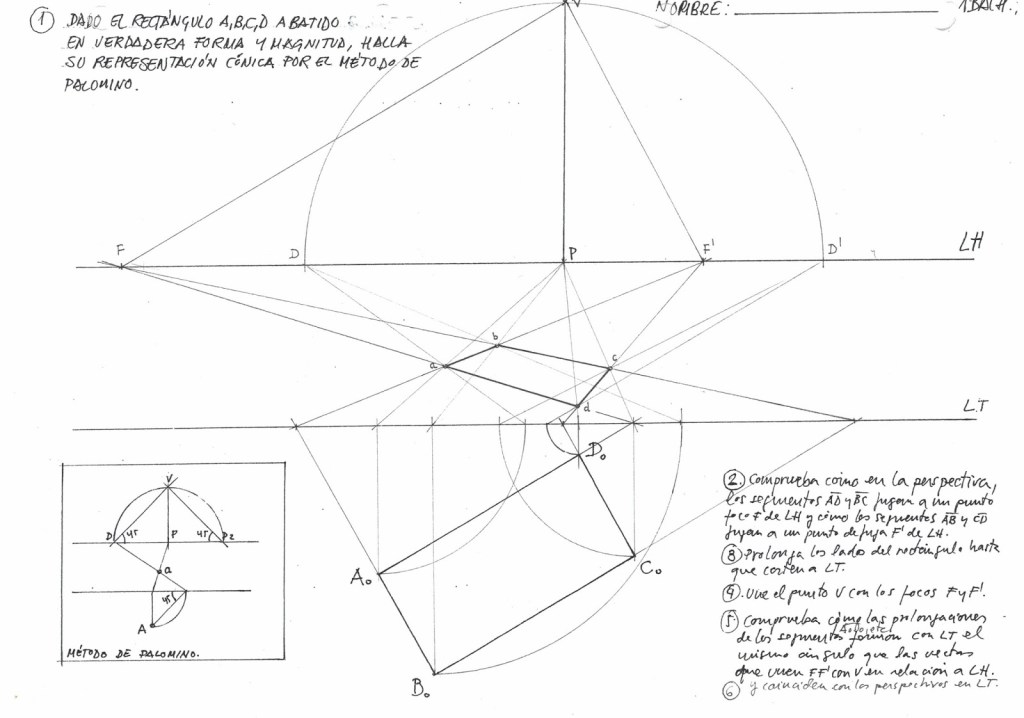
Para comenzar el tema, tenemos que entender que a partir de ahora, no s adentramos en el mundo de los Sistemas de Representación. Este sistema en concreto, el Sistema Cónico, supone un cambio de paradigma: pasamos de representar el objeto «tal como es» (medidas objetivas) a representarlo «tal como se ve» (percepción subjetiva).
La Perspectiva Cónica es la proyección central que mejor simula la visión humana, introduciendo la deformación espacial por la profundidad. A continuación, se detallan los conceptos teóricos fundamentales para la ejecución de las láminas de clase.
1. Elementos Fundamentales del Sistema
Para construir una perspectiva cónica, debemos definir espacialmente la posición del observador respecto al objeto y al plano de dibujo.
- Punto de Vista (V): Corresponde a la posición del ojo del observador. Determina el centro de la proyección.
- Plano del Cuadro (PC): Es el plano vertical imaginario sobre el cual se proyecta el dibujo (situado entre el observador y el objeto).
- Plano Geometral (PG): Es el plano horizontal (suelo) sobre el que se apoyan tanto el observador como los objetos a representar.
- Línea de Tierra (LT): Es la intersección del Plano del Cuadro con el Plano Geometral. Importante: Es la única línea del dibujo donde las medidas de anchura y altura se encuentran en Verdadera Magnitud.
- Línea de Horizonte (LH): Es la recta horizontal situada a la altura del Punto de Vista. Geométrica y conceptualmente, representa el «lugar geométrico» donde convergen todas las rectas horizontales paralelas entre sí (el infinito).

2. Clasificación de la Perspectiva
La posición del objeto respecto al Plano del Cuadro determina el tipo de perspectiva:
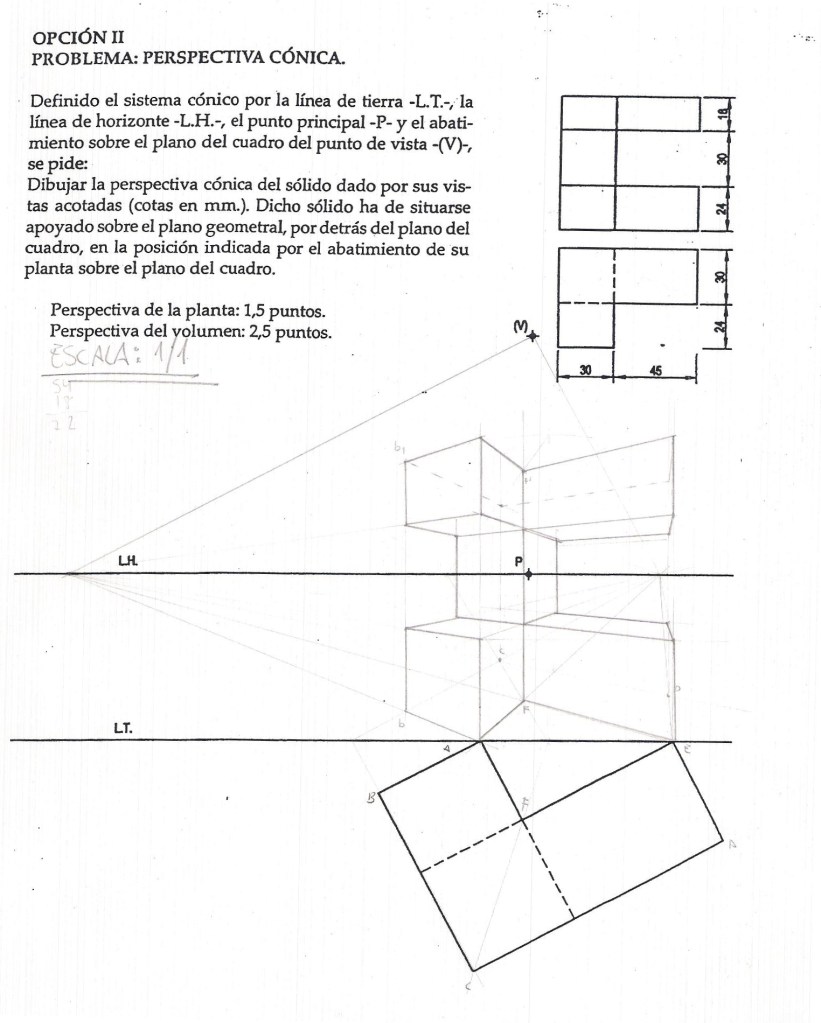
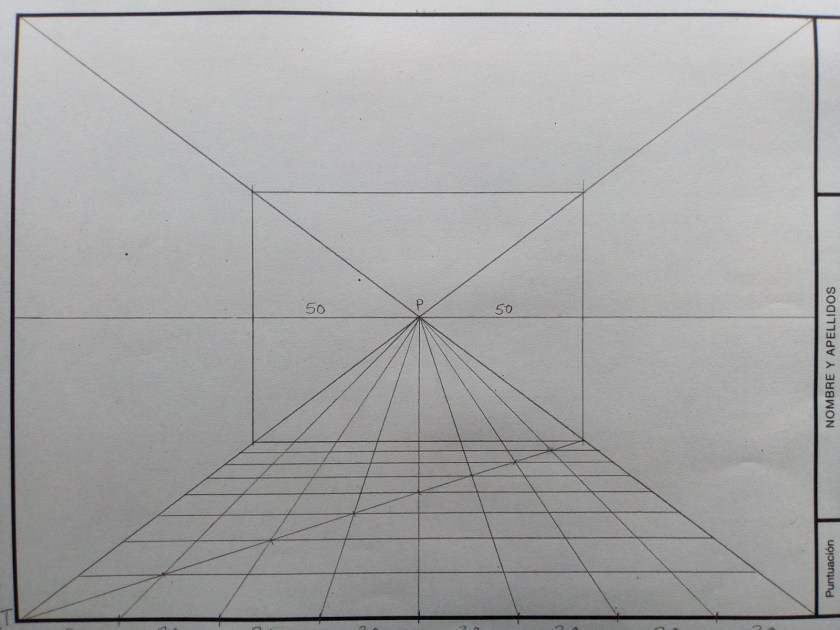
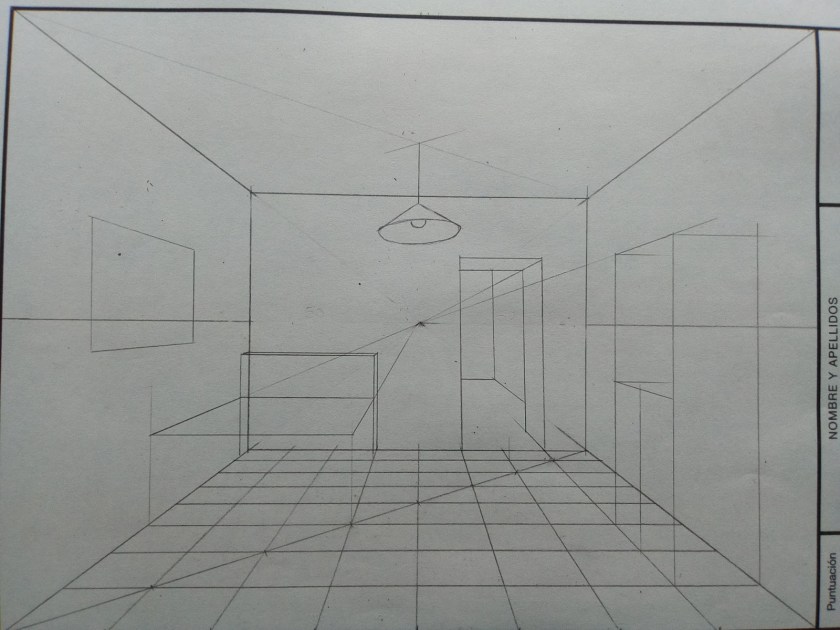
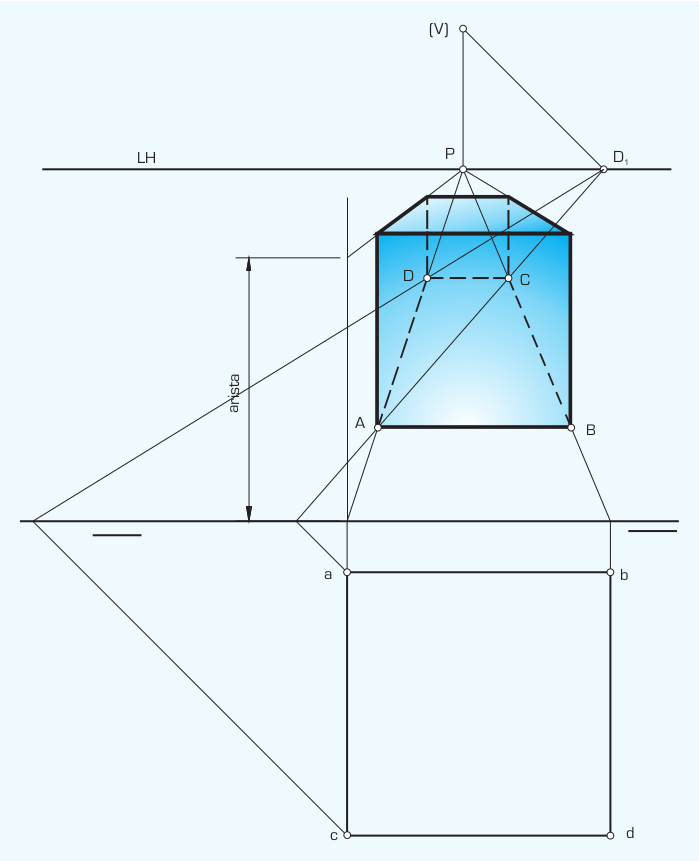
A. Perspectiva Cónica Frontal (Un Punto de Fuga)
Ocurre cuando una de las caras principales del objeto es paralela al Plano del Cuadro.
- Las líneas horizontales y verticales de esa cara se mantienen paralelas y perpendiculares en el dibujo (no fugan).
- Las líneas perpendiculares al plano del cuadro (profundidad) convergen en un único punto situado en la Línea de Horizonte: el Punto Principal (P).
- Para medir profundidades se utilizan los Puntos de Distancia (D y D’).
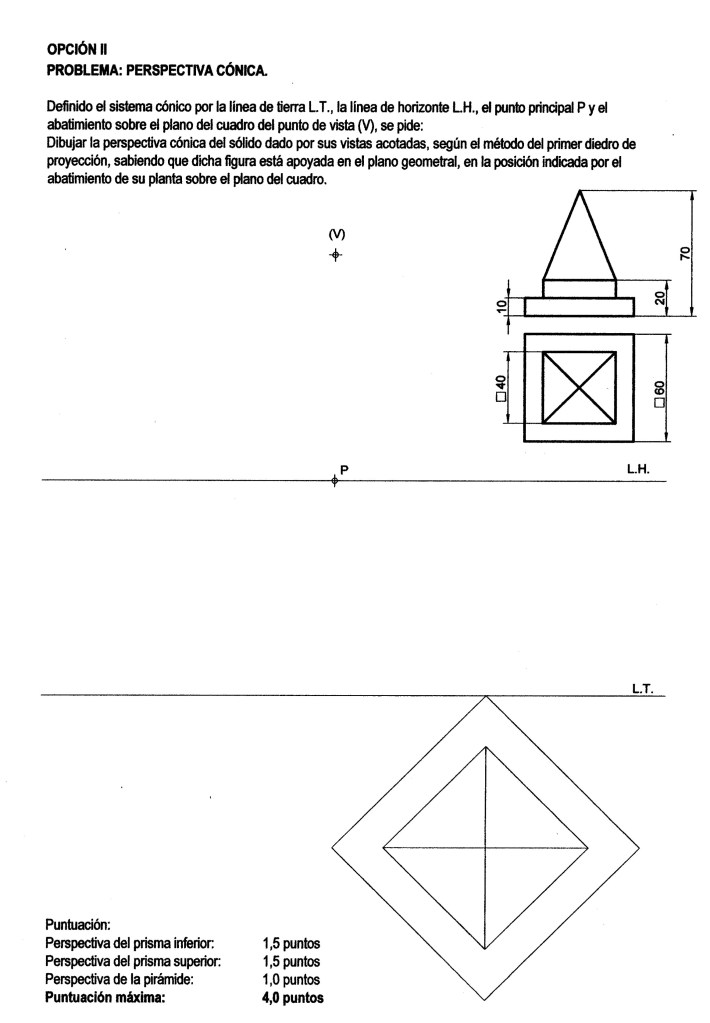
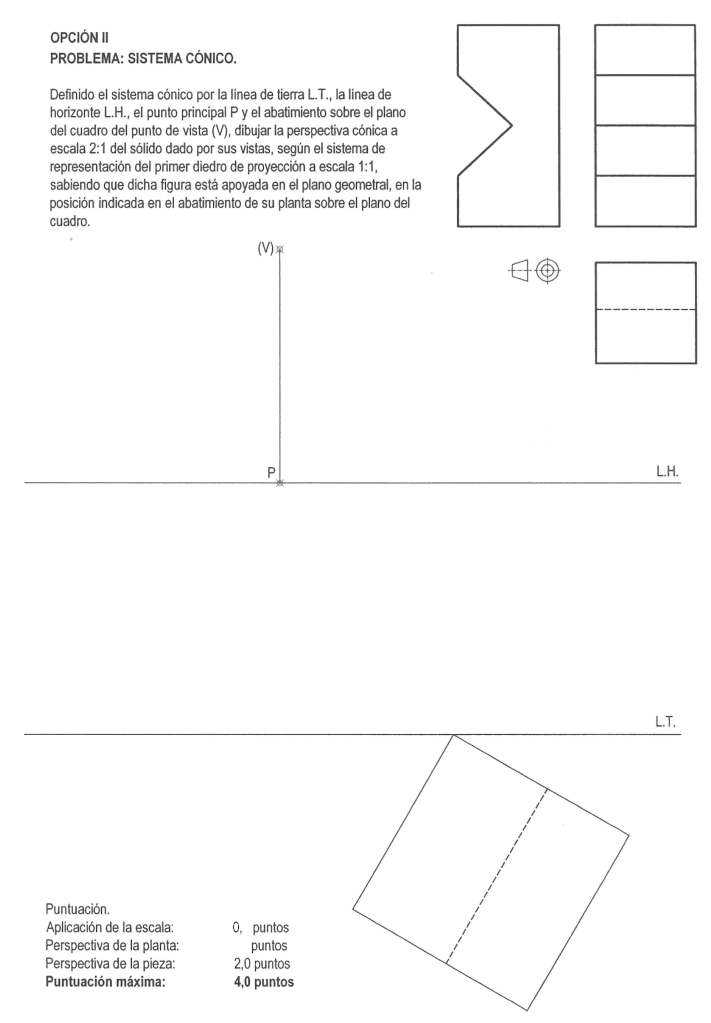
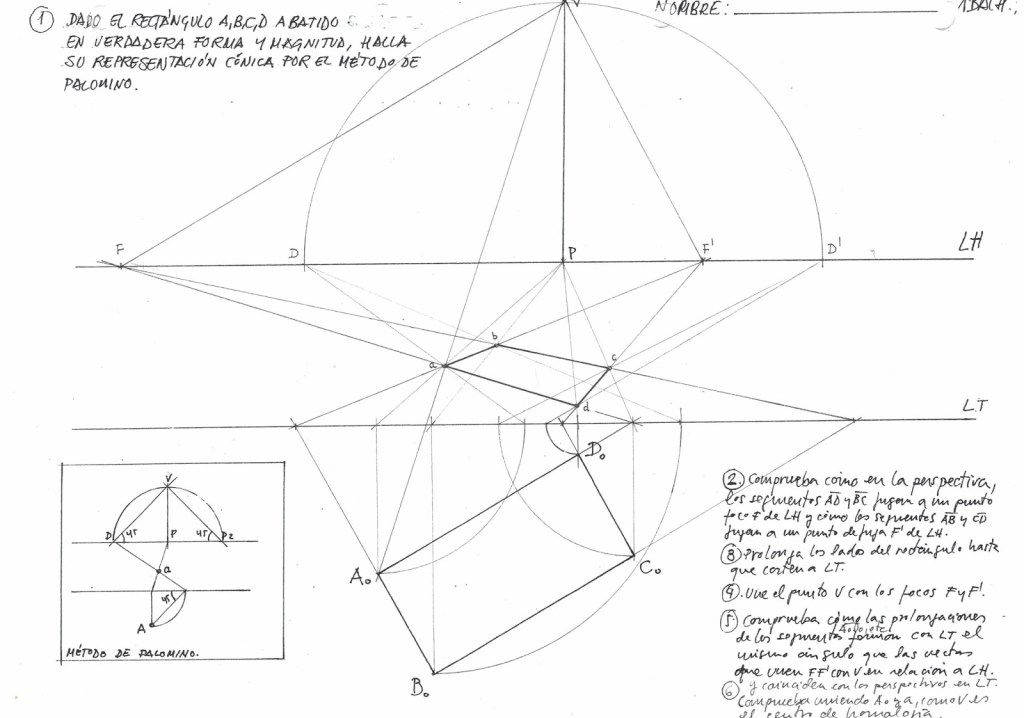
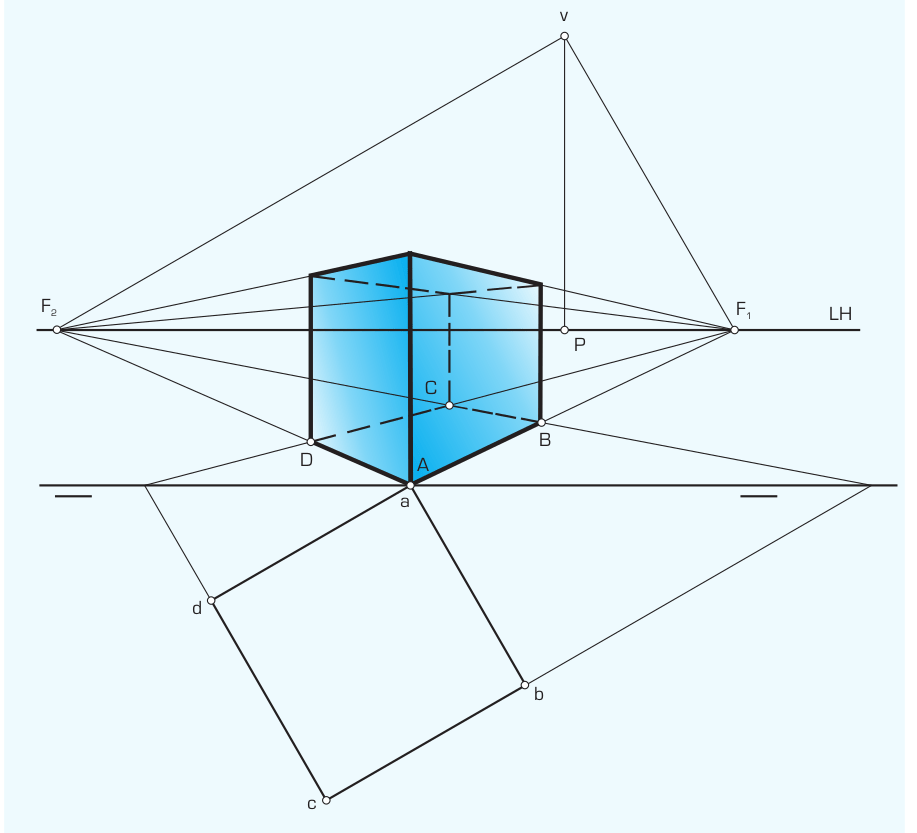
B. Perspectiva Cónica Oblicua (Dos Puntos de Fuga)
Ocurre cuando el objeto se sitúa de forma angular respecto al Plano del Cuadro.
- No hay caras paralelas al espectador; vemos el objeto «desde una arista».
- Las aristas horizontales fugan hacia dos puntos situados en la Línea de Horizonte: Foco derecho (F) y Foco izquierdo (F’).
- Las aristas verticales se mantienen perpendiculares a la Línea de Tierra.
3. Visualiza en Diédrico para ver en Cónica
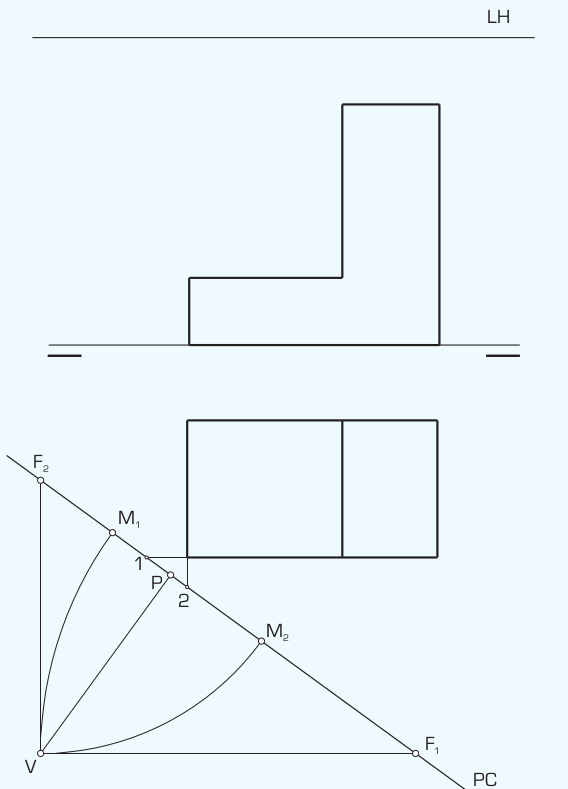
En este esquema puedes ver la disposición que tendría el observador (V) frente al «edificio». Su ángulo de visión abarca desde un punto de fuga al otro (F1-F2) y el punto (P) es el punto Principal sobre el Plano del Cuadro. El «Edificio» está por detrás del plano del cuadro, y con una disposición que permite ver ambas fachadas bajo un ángulo de 60-30º. También aparecen los puntos métricos, que nos ayudarán a realizar el ejercicio en caso que alguno de los puntos de fuga quede fuera del espacio de trabajo. Trasladando toda esa información sobre la Línea de Tierra y la Línea de Horozonte, el resultado debería ser algo así:
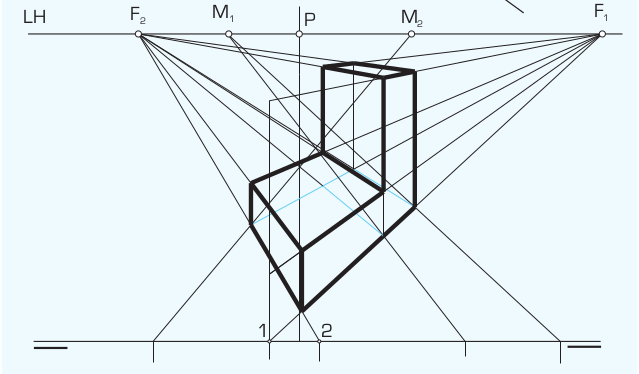
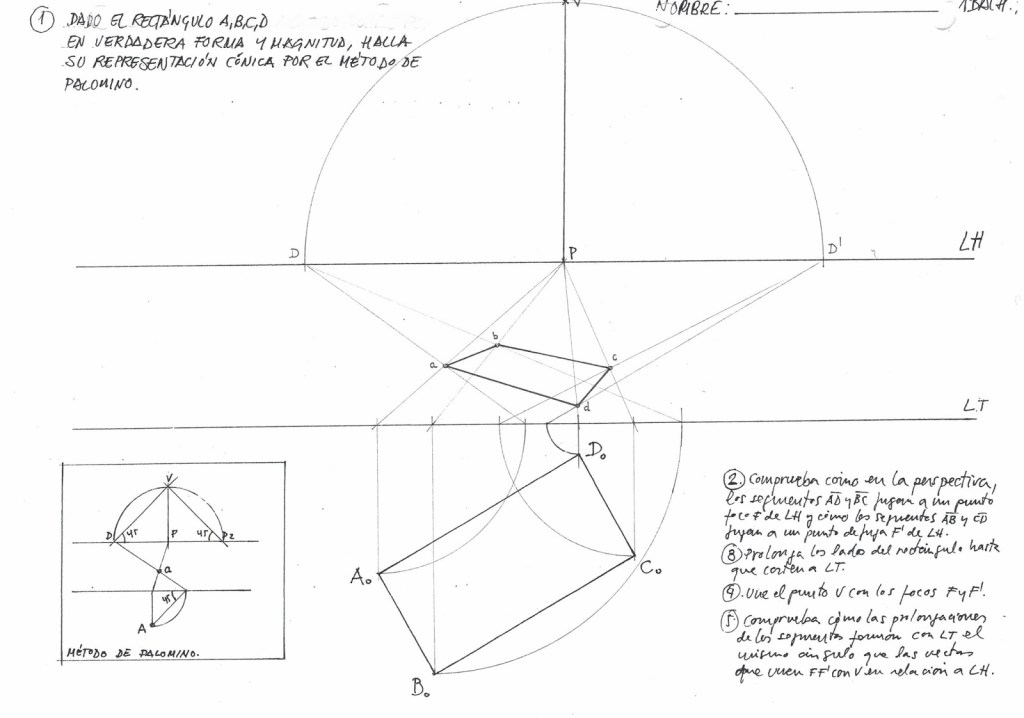
4. La Cónica como Transformación Homológica
Tal y como discutimos en las sesiones anteriores, existe una relación matemática directa entre la geometría plana y la proyectiva. La obtención de la perspectiva de una planta (suelo) no es más que una Homología que transforma una figura real (generalmente ortogonal) en una figura deformada por la perspectiva.
Para los que os gusta aplicar la lógica matemática en lugar de la memorización mecánica, esta es la correspondencia de elementos:
| Elemento en el Sistema Cónico | Elemento equivalente en Homología | Función |
| Línea de Tierra (LT) | Eje de Homología | Lugar de puntos dobles. Lo que toca esta línea no sufre transformación. |
| Línea de Horizonte (LH) | Recta Límite | Lugar geométrico de los puntos del infinito. |
| Punto de Vista abatido (V) | Centro de Homología | Origen de los rayos proyectantes. |
| Puntos de Fuga (F, F’) | Puntos homólogos del infinito | Destino de las rectas paralelas. |
Recuerda: Cuando buscamos un punto de fuga de una recta, estamos realizando la operación de hallar el homólogo de su punto impropio (infinito) mediante la paralela trazada desde el Centro de Homología (V) hasta la Recta Límite (LH).
5. Consideraciones para el Trazado
Para la correcta resolución de los ejercicios propuestos en el aula, tenemos que tener en cuenta lo siguiente:
- Verticalidad: En la cónica frontal y oblicua (de 2 puntos), todas las líneas de altura del objeto real deben dibujarse perfectamente perpendiculares a la Línea de Tierra.
- Medición: Las alturas reales solo pueden tomarse sobre la Línea de Tierra y trasladarse mediante fugas.
- Precisión: El grosor del lápiz influye. Hay que ser rigurosos con los encuentros de líneas en los puntos de fuga para evitar errores acumulativos en el dibujo final.
6. Láminas y ejercicios solucionados